前言
sstable 文件的foot, data block 和index block都已经介绍过了,看起来好像已经齐备了,根据footer 能够找到index block,而index记录了data block的索引信息,可以根据index block中的索引,快速定位到某个key(可能)位于which data block。
那么meta block和metaindex block到底是干啥的呢,为什么要有它呢?meta block的作用在于快速的确定,是否存在某个key,如果不存在,就没必要去遍历data block查找该key了。
如何快速判断某个key是否存在?
Bloom Filter这种数据结构就是干这个活的。
Bloom Filter
Burton Howard Bloom 在1970年设计的数据结构,用来判断某个key是否属于某个集合。它的原理比较简单,首先定义一个很大的数组,作为位图,初始时,位图中的每个元素都是0。向集合添加某个key的时候,计算一组hash值(多个不同的hash函数),根据结果将位图对应位置的位设为1。如下图所示:
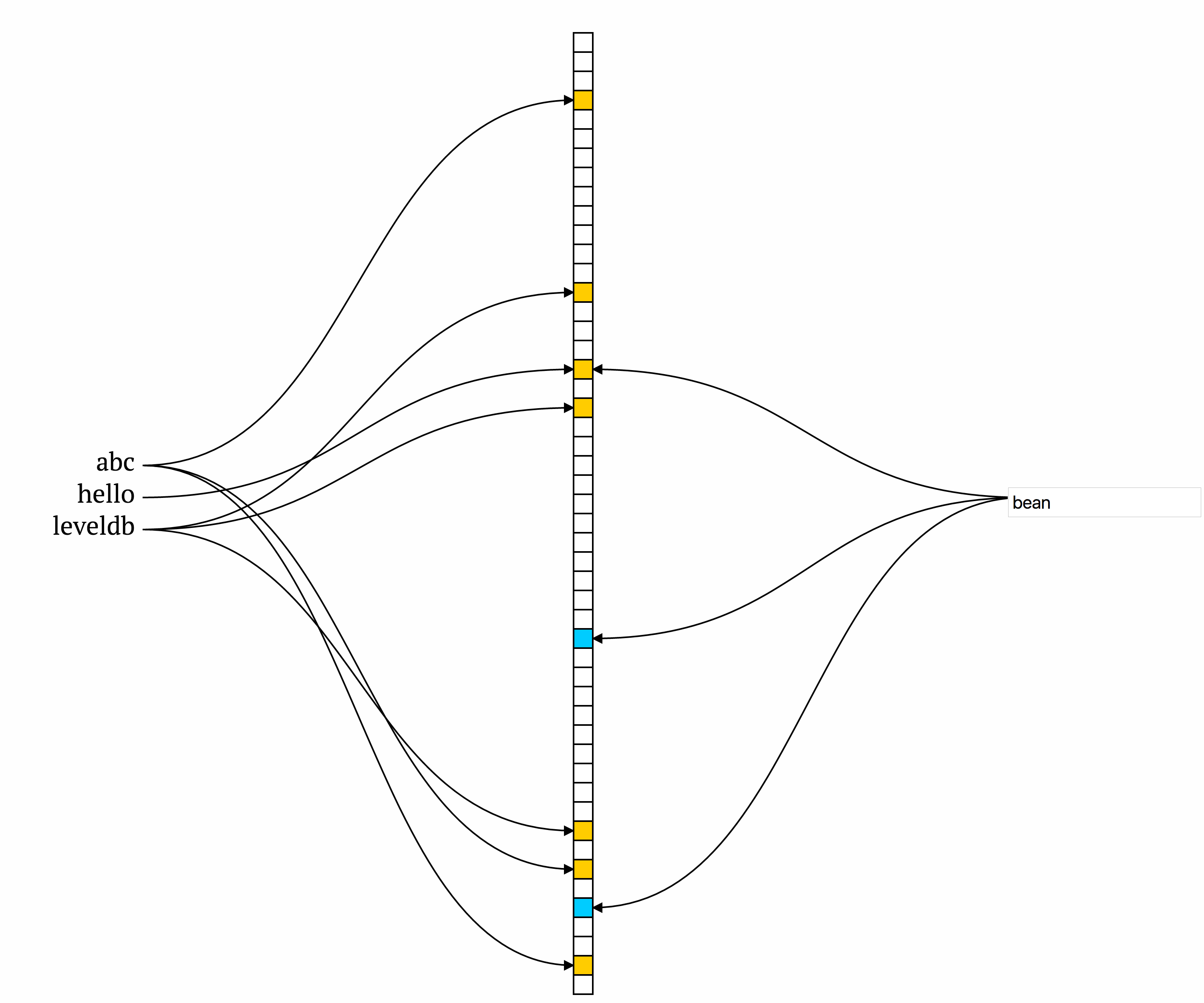
当判断某个key,如上图中的bean是否存在时,将key值通过多个hash函数(如上图中的3个hash函数),判断对应位置是否是1,如果不是1,表示该key并不存在。
如果将key值通过多个hash函数,发现每一个对应位置的bit都是1,说明该key值有很大的概率是存在的。
为什么是很大的概率,而不是绝对?因为Bloom Filter可能会出现虚警,发现每个对应位置都是1,但是去查找确实不存在该key,如下图所示:
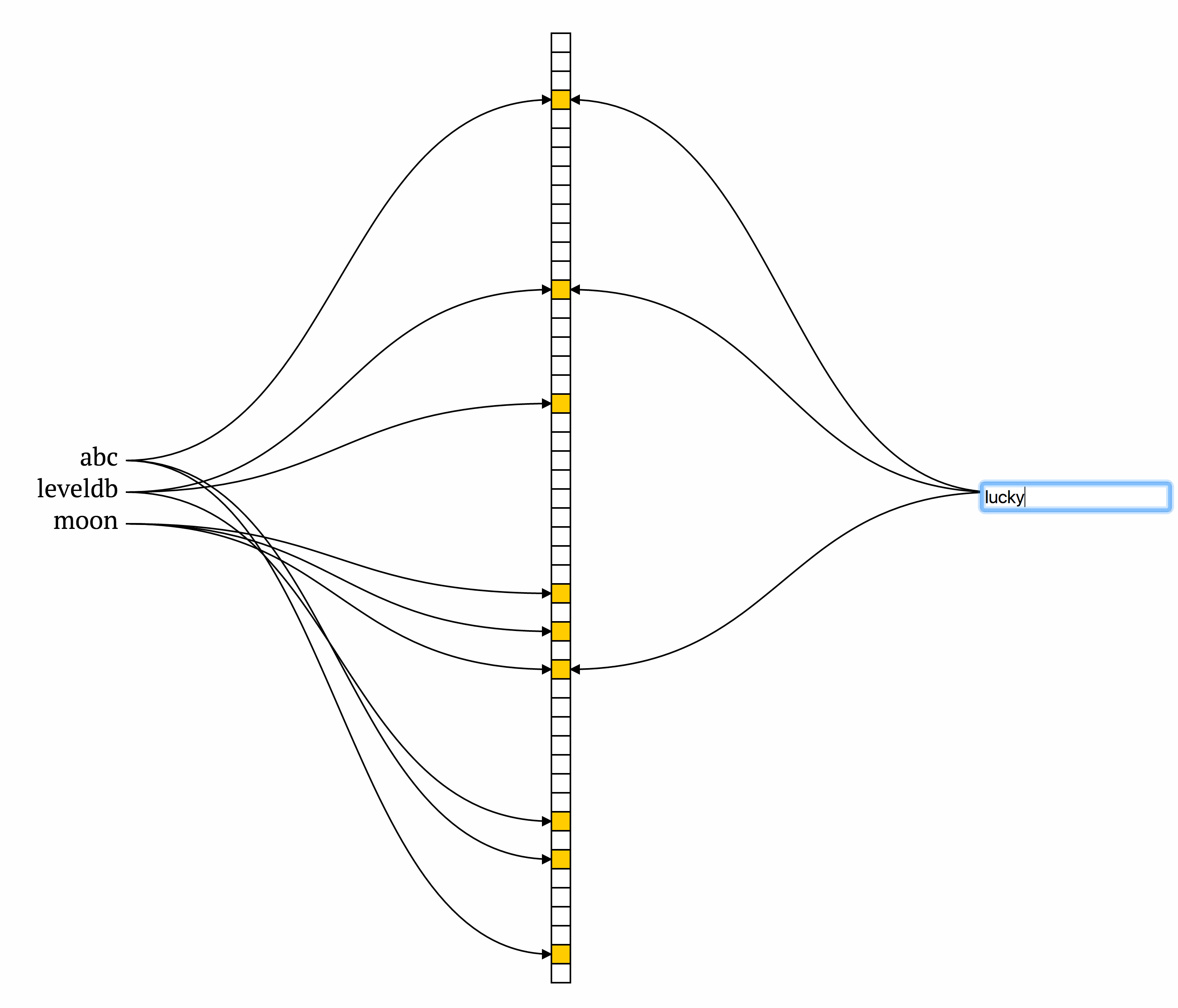
上图中lucky并不在集合中,但是hash算出来的三个位置,分别有abc leveldb moon将其设置为1,所以lucky被误判成存在集合中,造成false positive,出现虚警。
即bloom filter 有如下的性质:
- 如果bloom filter判断不在集合中,那么一定不在集合中 (Never false negative)
- 如果bloom filter判断在集合中,那么有很大的概率在集合中,但是也有一定的概率不在集合中,即出现虚警 (false positive)
既然会出现false positive,那么虚警概率就很重要了。考虑极端情况,如果位图数组相对于key的个数,太少,势必造成几乎每一个bit都是1,这样虚警的概率是非常高的,整个bloom filter压根就没有存在的价值,因为无论怎么判断,bloom filter总是回答key在集合中。
因此判断集合的大小,选择合适size的bloom filter位图就成了效率的关键。
如果位图中的bit数位为m,集合中的元素为n,hash函数的个数为k,那么虚警概率
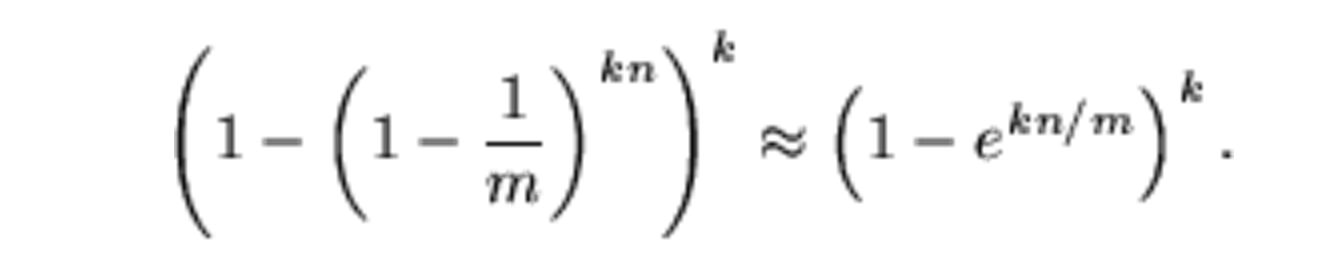
如果m 和n 是确定的,那么最优的k为:
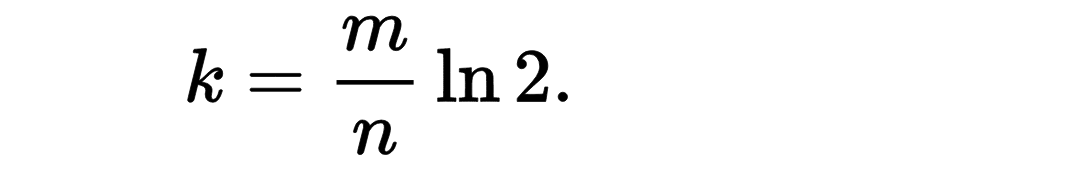
m n k 组合下,相关虚警概率的情况如下:
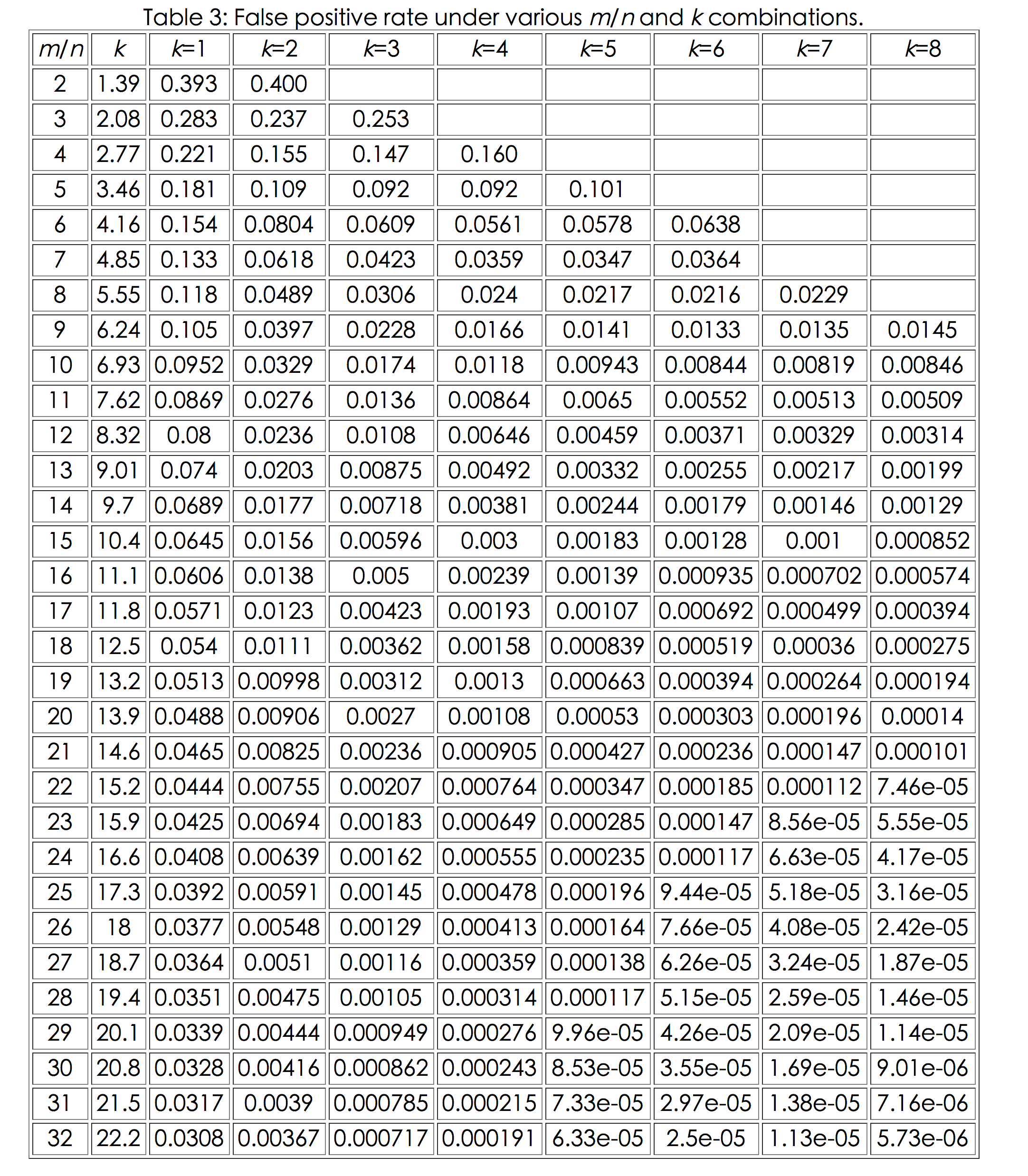
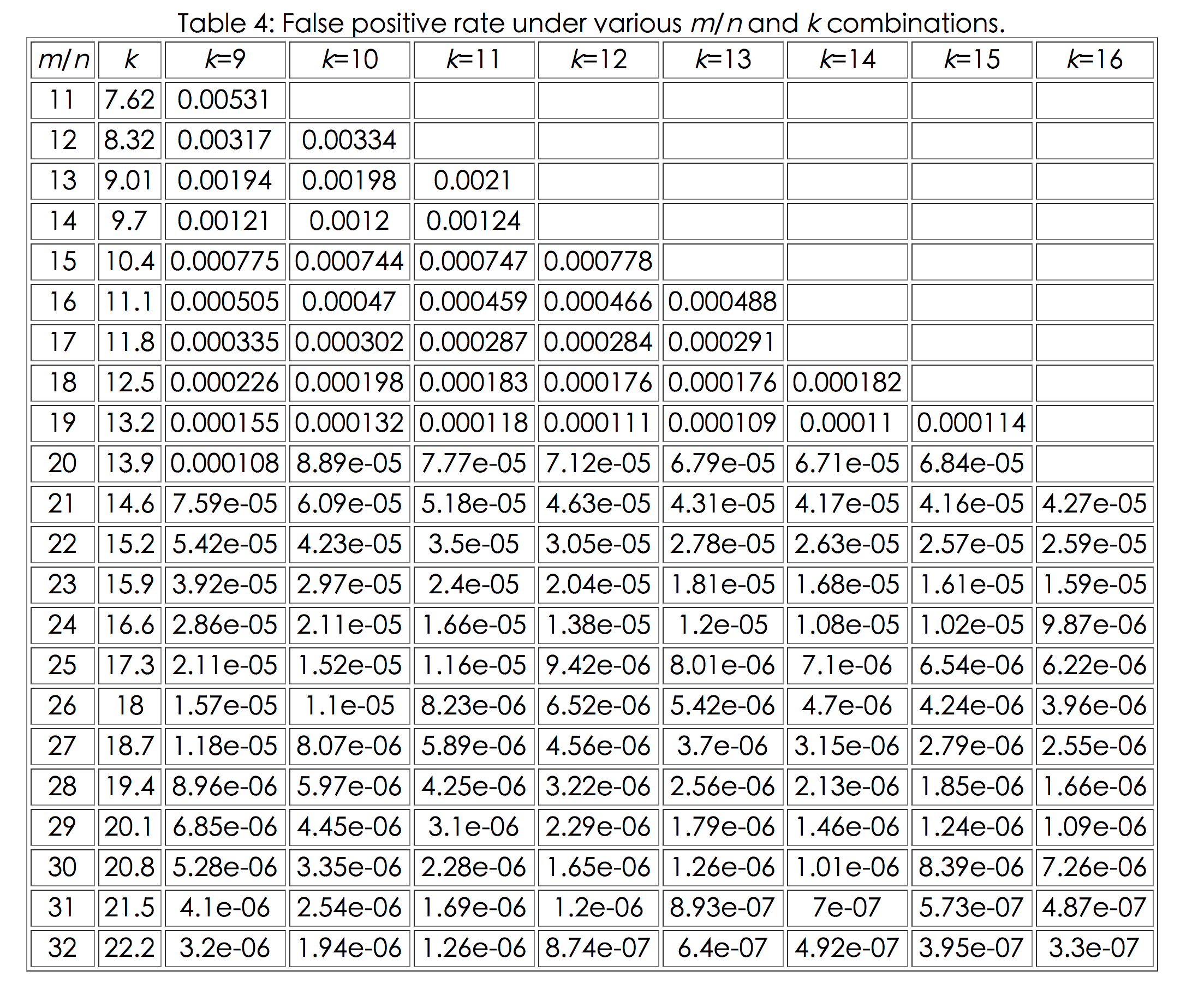

(数据来源于Bloom Filters - the math)
很明显,如果hash 函数的个数太多,就会带来更多的运算,这显然是不合理的,因此,要想降低虚警概率,必须要m/n要尽可能的大,
如果m/n等于20的时候,3个hash函数就可以将虚警概率降低到千分之三左右,4个hash 函数就能将虚警概率控制在千分之一左右。
leveldb中的bloom filter
leveldb搞个全局的Bloom Filter是不现实的,因为无法预知客户到底存放多少key,leveldb可能存放百万千万个key-value pair,也可能存放几百 几千个key-value,因为n不能确定范围,因此位图的大小m,也很难事先确定。
如果设置的m过大,势必造成内存浪费,如果设置的m过小,就会造成很大的虚警。
leveldb的设计,并不是全局的bloom filter,而是根据局部的bloom filter,每一部分的数据,设计出一个bloom filter,多个bloom filter来完成任务。
leveldb中的bloom filter有第二个层面的改进,即采用了下面论文中的算法思想:
Less Hashing, Same Performance: Building a Better Bloom Filter
这个论文有兴趣的筒子可以读一下,我简单summary一下论文的思想,为了尽可能的降低虚概率,最优的hash函数个数可能很高,比如需要10个hash函数,这势必带来很多的计算,而且要设计多个不同的hash函数,论文提供了一个思想,用1个hash函数,多次移位和加法,达到多个hash 的结果。
代码解读
static uint32_t BloomHash(const Slice& key) // 哈希函数
{
return Hash(key.data(), key.size(), 0xbc9f1d34);
}
class BloomFilterPolicy : public FilterPolicy
{
private:
size_t bits_per_key_; // 一个key占多少位
size_t k_; // 哈希函数个数
public:
explicit BloomFilterPolicy(int bits_per_key): bits_per_key_(bits_per_key)
{
// We intentionally round down to reduce probing cost a little bit
k_ = static_cast<size_t>(bits_per_key * 0.69); // 0.69 =~ ln(2)
if (k_ < 1) k_ = 1;
if (k_ > 30) k_ = 30;
}
virtual const char* Name() const
{
return "leveldb.BuiltinBloomFilter2";
}
// n:key的个数;dst:存放过滤器处理的结果
virtual void CreateFilter(const Slice* keys, int n, std::string* dst) const
{
// Compute bloom filter size (in both bits and bytes)
size_t bits = n * bits_per_key_;
// For small n, we can see a very high false positive rate. Fix it
// by enforcing a minimum bloom filter length.
// 位列bits最小64位,8个字节
if (bits < 64) bits = 64;
// bits位占多少个字节
size_t bytes = (bits + 7) / 8;
// 得到真实的位列bits
bits = bytes * 8;
const size_t init_size = dst->size();
dst->resize(init_size + bytes, 0);
// 在过滤器集合最后记录需要k_次哈希
dst->push_back(static_cast<char>(k_)); // Remember # of probes in filter
char* array = &(*dst)[init_size];
for (size_t i = 0; i < n; i++)
{
// Use double-hashing to generate a sequence of hash values.
// See analysis in [Kirsch,Mitzenmacher 2006].
uint32_t h = BloomHash(keys[i]);
const uint32_t delta = (h >> 17) | (h << 15); // Rotate right 17 bits
// 使用k个哈希函数,计算出k位,每位都赋值为1。
// 为了减少哈希冲突,减少误判。
for (size_t j = 0; j < k_; j++)
{
// 得到元素在位列bits中的位置
const uint32_t bitpos = h % bits;
/*
bitpos/8计算元素在第几个字节;
(1 << (bitpos % 8))计算元素在字节的第几位;
例如:
bitpos的值为3, 则元素在第一个字节的第三位上,那么这位上应该赋值为1。
bitpos的值为11,则元素在第二个字节的第三位上,那么这位上应该赋值为1。
为什么要用|=运算,因为字节位上的值可能为1,那么新值赋值,还需要保留原来的值。
*/
array[bitpos/8] |= (1 << (bitpos % 8));
h += delta;
}
}
}
virtual bool KeyMayMatch(const Slice& key, const Slice& bloom_filter) const
{
const size_t len = bloom_filter.size();
if (len < 2) return false;
const char* array = bloom_filter.data();
const size_t bits = (len - 1) * 8;
// Use the encoded k so that we can read filters generated by
// bloom filters created using different parameters.
const size_t k = array[len-1];
if (k > 30)
{
// 为短bloom filter保留,当前认为直接match
// Reserved for potentially new encodings for short bloom filters.
// Consider it a match.
return true;
}
uint32_t h = BloomHash(key);
const uint32_t delta = (h >> 17) | (h << 15); // Rotate right 17 bits
for (size_t j = 0; j < k; j++)
{
const uint32_t bitpos = h % bits;
// 只要有一位为0,说明元素肯定不在过滤器集合内。
if ((array[bitpos/8] & (1 << (bitpos % 8))) == 0) return false;
h += delta;
}
return true;
}
};
我们先来搞定产生Bloom Filter的算法,然后来看调用Bloom Filter的时机。
输入是:
- keys : 本轮所有的key
- n : 本轮所有的key的个数
严格意义上讲,Leveldb Bloom Filter创建时只有一个参数即bits_per_key:
explicit BloomFilterPolicy(int bits_per_key): bits_per_key_(bits_per_key)
{
// We intentionally round down to reduce probing cost a little bit
k_ = static_cast<size_t>(bits_per_key * 0.69); // 0.69 =~ ln(2)
if (k_ < 1) k_ = 1;
if (k_ > 30) k_ = 30;
}
这个bits_per_key是何意呢? 它即是前文原理部分介绍的 m/n,位图bit数除以key的个数,这个参数是创建BloomFilterPolicy的唯一一个入参,按照我们的表格,bits_per_key越大越好。
有了这个值,就有最优的k值,即:
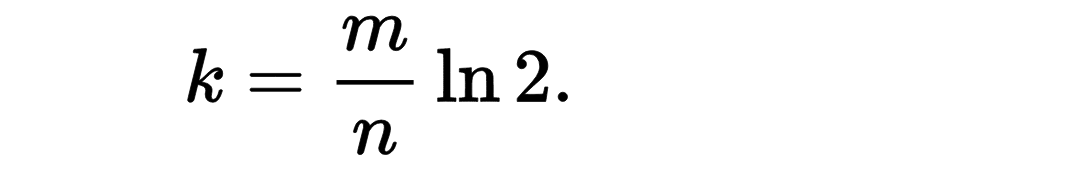
即我们看到的:
k_ = static_cast<size_t>(bits_per_key * 0.69); // 0.69 =~ ln(2)
目前有了m/n的值,根据key的个数n,就可以计算出最优的bit数,即m的值:
// Compute bloom filter size (in both bits and bytes)
size_t bits = n * bits_per_key_;
// For small n, we can see a very high false positive rate. Fix it
// by enforcing a minimum bloom filter length.
// 位列bits最小64位,8个字节
if (bits < 64) bits = 64;
// bits位占多少个字节
size_t bytes = (bits + 7) / 8;
// 得到真实的位列bits
bits = bytes * 8; /*bits即 位图中bit的个数*/
剩下的事情就水到渠成了,对于每个key,计算k次,将对应位置的bit设置成1:
外层循环是每一个key值
for (size_t i = 0; i < n; i++)
{
// Use double-hashing to generate a sequence of hash values.
// See analysis in [Kirsch,Mitzenmacher 2006].
uint32_t h = BloomHash(keys[i]);
const uint32_t delta = (h >> 17) | (h << 15); // Rotate right 17 bits
/* 内层循环是对每一个key计算k次hash,当然用的是前面提到的论文中的思想。*/
for (size_t j = 0; j < k_; j++)
{
// 得到元素在位列bits中的位置
const uint32_t bitpos = h % bits;
array[bitpos/8] |= (1 << (bitpos % 8));
h += delta;
}
}
}
注意,因为sstable中key的个数可能很多,当攒了足够多个key值,就会计算一批位图,再攒一批key,又计算一批位图,那么这么多bloom filter的位图,必需分隔开,否则就混了。
也就说,位图与位图的边界必需清晰,否则就乱了。看下面代码注释:
void FilterBlockBuilder::GenerateFilter() {
const size_t num_keys = start_.size();
if (num_keys == 0) {
// Fast path if there are no keys for this filter
filter_offsets_.push_back(result_.size());
return;
}
// Make list of keys from flattened key structure
start_.push_back(keys_.size()); // Simplify length computation
tmp_keys_.resize(num_keys);
/*得到本轮的所有的keys,放入tmp_keys_数组*/
for (size_t i = 0; i < num_keys; i++) {
const char* base = keys_.data() + start_[i];
size_t length = start_[i+1] - start_[i];
tmp_keys_[i] = Slice(base, length);
}
// Generate filter for current set of keys and append to result_.
/*先记录下上一轮位图截止位置,防止位图的边界混淆*/
filter_offsets_.push_back(result_.size());
/*将本轮keys计算得来的位图追加到result_字符串*/
policy_->CreateFilter(&tmp_keys_[0], static_cast<int>(num_keys), &result_);
tmp_keys_.clear();
keys_.clear();
start_.clear();
}
当TableBuilder 每次增加一个元素的时候,就会调用:
void FilterBlockBuilder::AddKey(const Slice& key) {
Slice k = key;
start_.push_back(keys_.size());
keys_.append(k.data(), k.size());
}
我们看下FilterBlockBuilder的定义:
class FilterBlockBuilder {
public:
explicit FilterBlockBuilder(const FilterPolicy*);
void StartBlock(uint64_t block_offset);
void AddKey(const Slice& key);
Slice Finish();
private:
void GenerateFilter();
const FilterPolicy* policy_;
/*注意本轮keys产生的位图计算完毕后,会将keys_, start_ ,还有tmp_keys_ 清空*/
std::string keys_; // 暂时存放本轮所有keys,追加往后写入
std::vector<size_t> start_; // 记录本轮key与key之间的边界的位置,便于分割成多个key
std::string result_; // 计算出来的位图,多轮计算则往后追加写入
std::vector<Slice> tmp_keys_; // 将本轮的所有key,存入该vector,其实并无存在的必要,用临时变量即可
std::vector<uint32_t> filter_offsets_; //计算出来的多个位图的边界位置,用于分隔多轮keys产生的位图
// No copying allowed
FilterBlockBuilder(const FilterBlockBuilder&);
void operator=(const FilterBlockBuilder&);
};
我们终于提到了多轮了,既然有轮次的概念,那么问题就来了,啥时候发起一轮keys位图的计算?
接下来我们看为一轮多个时机
void FilterBlockBuilder::StartBlock(uint64_t block_offset) {
uint64_t filter_index = (block_offset / kFilterBase);
assert(filter_index >= filter_offsets_.size());
while (filter_index > filter_offsets_.size()) {
GenerateFilter();
}
}
这个函数负责一轮计算Bloom Filter的位图。
触发的时机是Flush函数,而Flush的时机是预测Data Block的size超过options.block_size
void TableBuilder::Add(const Slice& key, const Slice& value) {
Rep* r = rep_;
assert(!r->closed);
if (!ok()) return;
if (r->num_entries > 0) {
assert(r->options.comparator->Compare(key, Slice(r->last_key)) > 0);
}
if (r->pending_index_entry) {
assert(r->data_block.empty());
r->options.comparator->FindShortestSeparator(&r->last_key, key);
std::string handle_encoding;
r->pending_handle.EncodeTo(&handle_encoding);
r->index_block.Add(r->last_key, Slice(handle_encoding));
r->pending_index_entry = false;
}
if (r->filter_block != NULL) {
r->filter_block->AddKey(key);
}
r->last_key.assign(key.data(), key.size());
r->num_entries++;
r->data_block.Add(key, value);
const size_t estimated_block_size = r->data_block.CurrentSizeEstimate();
if (estimated_block_size >= r->options.block_size) {
Flush();
}
}
void TableBuilder::Flush() {
Rep* r = rep_;
assert(!r->closed);
if (!ok()) return;
if (r->data_block.empty()) return;
assert(!r->pending_index_entry);
WriteBlock(&r->data_block, &r->pending_handle);
if (ok()) {
r->pending_index_entry = true;
r->status = r->file->Flush();
}
if (r->filter_block != NULL) {
r->filter_block->StartBlock(r->offset);
}
}
有一个不容易理解的地方是有一个参数2KB
static const size_t kFilterBaseLg = 11;
static const size_t kFilterBase = 1 << kFilterBaseLg;
void FilterBlockBuilder::StartBlock(uint64_t block_offset) {
uint64_t filter_index = (block_offset / kFilterBase);
assert(filter_index >= filter_offsets_.size());
while (filter_index > filter_offsets_.size()) {
GenerateFilter();
}
}
这个参数的本意应该是,如果多个key-value的总长度超过了2KB,我就应该计算这些key的位图了。但是无奈发起的时机是有Flush决定,因此,并非2KB的数据就会发起一轮 Bloom Filter的计算,比如block_offset等于7KB,可能造成多轮的GenerateFilter函数调用,而除了第一轮的调用会产生位图,其它2轮相当于轮空,只是将result_的size再次放入filter_offsets_。
void FilterBlockBuilder::GenerateFilter() {
const size_t num_keys = start_.size();
if (num_keys == 0) {
// Fast path if there are no keys for this filter
filter_offsets_.push_back(result_.size());
return;
}
...
}
势必造成如下图的结果:
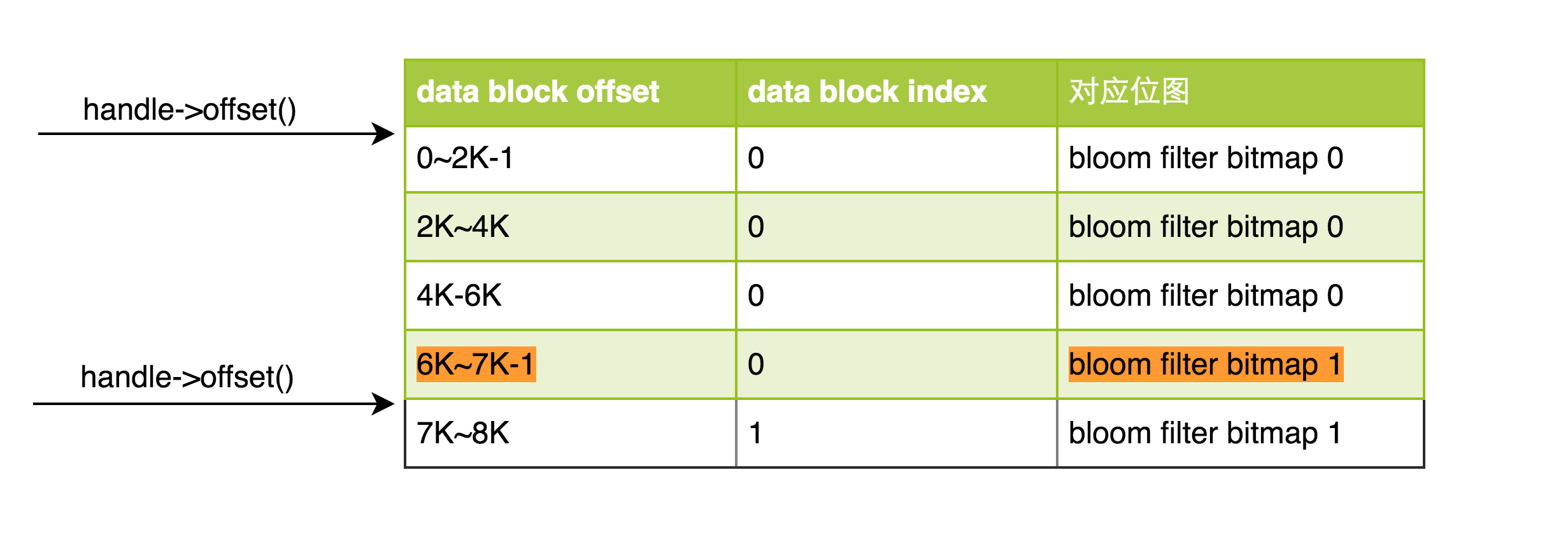
如果(0~7K-1)是第一个data block的范围,(7K~14K-1)是第二个 data block的范围,(0~6K-1)没啥问题,可是(6K~7K-1)属于第一个data block,但是存放bloom filter的时候,指向的是第二个 bloom filter,将来可能会带来问题。
实际上不会,因为 meta block是data block的辅助,应用层绝不会问 data block offset为6K的block位图在何方。从查找的途径来看,先根据key通过第二篇的index block,找到对应的data block,而data block的offset,只会是0或者7K,绝不会是6K。
当传入data block的offset是7K的时候,根据上表,就会返回第二个bloom filter,而第二个bloom filter会负责整个第二个data block的全部key,即data block的(7K~14K-1)范围内的所有key,都可以利用第二个bloom filter找到。
使用这种方法,当用户输入data block offset的时候,查找对应data block 的bloom filter bitmap非常方便:
bool FilterBlockReader::KeyMayMatch(uint64_t block_offset, const Slice& key) {
uint64_t index = block_offset >> base_lg_;
if (index < num_) {
uint32_t start = DecodeFixed32(offset_ + index*4);
uint32_t limit = DecodeFixed32(offset_ + index*4 + 4);
if (start <= limit && limit <= static_cast<size_t>(offset_ - data_)) {
Slice filter = Slice(data_ + start, limit - start);
return policy_->KeyMayMatch(key, filter);
} else if (start == limit) {
// Empty filters do not match any keys
return false;
}
}
return true; // Errors are treated as potential matches
}
按照上面的分析,如果block_offset为6KB的时候,就会找不到对应位图,因为 start和limit指向的都是bitmap 1,函数中的filter最终为空,但是没关系,绝不会传进来6K,因为6K不是两个data block的边界。
meta data的在SSTable File中的布局
TableBuilder::Finish函数中会将Filter Block落盘:
Status TableBuilder::Finish() {
Rep* r = rep_;
Flush();
assert(!r->closed);
r->closed = true;
BlockHandle filter_block_handle, metaindex_block_handle, index_block_handle;
// Write filter block
if (ok() && r->filter_block != NULL) {
/*将filter block写入磁盘*/
WriteRawBlock(r->filter_block->Finish(), kNoCompression,
&filter_block_handle);
}
// Write metaindex block
if (ok()) {
BlockBuilder meta_index_block(&r->options);
if (r->filter_block != NULL) {
// Add mapping from "filter.Name" to location of filter data
std::string key = "filter.";
key.append(r->options.filter_policy->Name());
std::string handle_encoding;
filter_block_handle.EncodeTo(&handle_encoding);
meta_index_block.Add(key, handle_encoding);
}
// TODO(postrelease): Add stats and other meta blocks
WriteBlock(&meta_index_block, &metaindex_block_handle);
}
Slice FilterBlockBuilder::Finish() {
if (!start_.empty()) {
GenerateFilter();
}
// Append array of per-filter offsets
const uint32_t array_offset = result_.size();
for (size_t i = 0; i < filter_offsets_.size(); i++) {
PutFixed32(&result_, filter_offsets_[i]);
}
PutFixed32(&result_, array_offset);
result_.push_back(kFilterBaseLg); // Save encoding parameter in result
return Slice(result_);
}
布局的方式如下图所示:
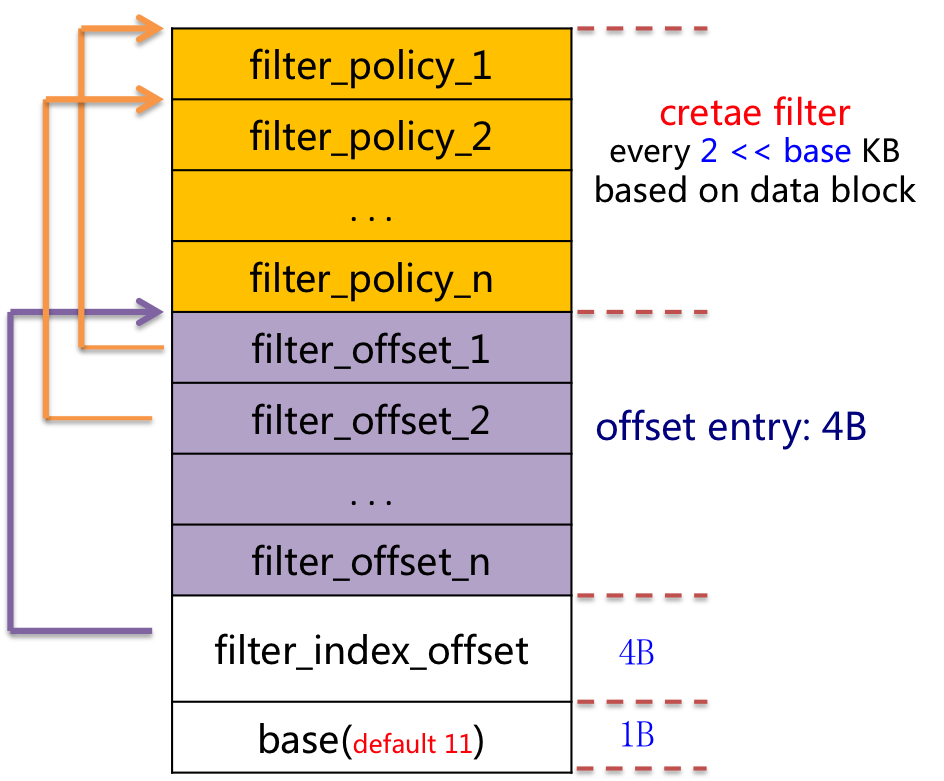
最后,metaindex_block 比较简单,格式和data block一模一样,只有一个key-value对,其中key值是filter.leveldb.BuiltinBloomFilter2, 而value,即meta data 所在的 BlockHandler,即位置信息。
也就说,metaindex_block 可以定位到 meta data的位置信息,即上图。